Starting date: fall 2024
Duration: 3 Years
Contat:
EDF R&D : Michail Korres (michail.korres@edf.fr), Vinicius Alves-Fernandes (vinicius.alves-fernandes@edf.fr), Irmela Zentner (irmela.zentner@edf.fr), Bertrand Iooss (bertrand.iooss@edf.fr)
CentraleSupélec (LMPS) : Fernando Lopez-Caballero (fernando.lopez-caballero@centralesupelec.fr), Filippo Gatti (filippo.gatti@centralesupelec.fr), Didier Clouteau (didier.clouteau@centralesupelec.fr)
Industrial context and scientific objectives
The seismic safety assessment of structures and components of nuclear power plants is based on a well-established methodology consisting in the (i) establishment of the site-specific seismic hazard, the (ii) computation of the dynamic response of structures interacting with the surrounding soil to compute seismic demand, the iii) evaluation of the seismic fragility of structures and components and iv) the convolution of hazard and fragility for safety assessment.
The development of best-estimate approaches together with comprehensive consideration of uncertainties as well as the development of integrated approaches from hazard to structural response allow for more accurate risk estimates (e.g. SINAPS@[1] and METIS[2] research projects). Recently, an integrated methodology was proposed by Korres et al. [1] accounting for the seismic wave propagation, from the source, through the complex geological medium in the regional and local scale of the site under consideration, and up to the structure’s foundation and its transmission to the sensitive equipment of interest (e.g., electro-mechanical devices, piping systems, etc.). However, the link between physics-based simulation and regulatory approaches where seismic load is defined by response spectra still needs to be fully established. On the other hand, source-to-structure 3D simulation remain computationally expensive and requires the development of surrogate models in particular in the light of uncertainty propagation and sensitivity analysis.
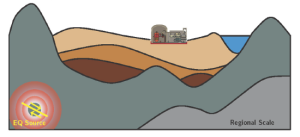
Figure 1. Source-to-structure wave propagation.
In this context, the main objective of this work is to develop a global methodology for seismic assessment of structures integrating: (i) a source-to-structure wave propagation modeling conditioned on the site-specific seismic hazard defined on the outcropping rock, and (ii) uncertainties at the different scales, while propagating them through the different steps of the procedure.
The proposed strategy for this PhD work is based on ideas synthesized in the following :
- Source-to-structure 3D physics-based simulations (PBS):
In order to appropriately model the seismic wave propagation at the different scales of analysis (regional scale km, site/structure scale m), a spectral element (SEM) – finite element method (FEM) coupling based on the domain reduction method [2, 3] already implemented in [1] is used as a basis for the numerical simulations. In this context, important components of the source-to-structure wave propagation [4, 5, 6] can be explicitly taken into account.
More precisely, such numerical approach requires : i) the definition of a realistic 3D geology (regional/local scale) and the mechanical properties of the structure [7, 8], ii) the characterization and modeling of the excitation source on the regional scale [9, 10], iii) the definition of the ground motion on the scale of the site (hazard analysis – [11, 12], iv) the constitutive model for the description of soil’s or structure’s behavior (structural analysis – [4]), and v) the way that the dynamic excitation is imposed as an input to the soil-structure interaction model [5, 13];
 |
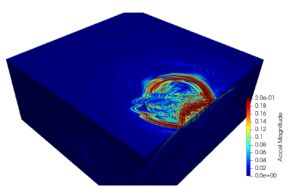 |
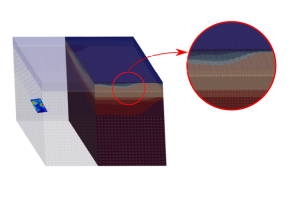
Figure 2. Large scale simulation: Regional geology detail (left), spatial variability of the seismic ground motion (right).
- Uncertainty quantification and propagation:
Uncertainties in the source-to-structure wave propagation modeling need also to be considered [14]. In this context, several studies have been proposed in the literature in order to account for these uncertainties : i) random fields for material properties [15, 16], ii) source modelling variability [17, 18], iii) sensitivity analysis for constitutive law parameters [19], iv) influence of the input motion excitation [3, 1].
Since hundreds to thousands of simulations are necessary for uncertainty propagation analyses in Monte-Carlo or more advances sampling strategies, surrogate models (Gaussian processes, Kriging, Polynomial chaos, etc.) can be constructed to obtain robust estimates of intensity measures (IM) [15] based on a reduced set of numerically costly high-fidelity simulations.
- Site-specific hazard definition on the outcropping rock:
Finally, to account for the site-specific hazard definition, ground motion generated from the 3D PBS simulation need to comply with the seismic hazard defined at the outcropping rock. Hazard is generally determined using a probabilistic seismic hazard analysis (PSHA), where the seismic ground motion is defined by seismic response spectra The latter are an input for our analysis. An ultimate objective of this work is to create a link between the ground motion defined at the outcropping rock, and the response spectrum at the structural level, used for the verification of structural and non-structural components.
The proposed strategy for this PhD work is synthesized in the following Figure 3.
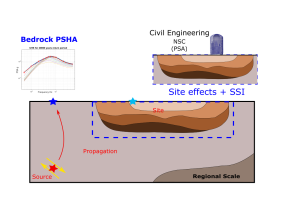
Figure 3. Thesis framework
Requirements
A successful candidate shall dispose strong knowledge in the following fields:
- Structural dynamics and numerical methods (finite elements)
- Parallel computing and programming
- Statistics and probabilities, uncertainty modelling
- Engineering seismology
A first experience in finite element modeling and parallel computing is appreciated.
Application procedure
Please submit electronically (in PDF format):
- a detailed resume
- a motivation letter
References
| [1] | M. Korres, F. Lopez-Caballero, V. Alves Fernandes, F. Gatti, I. Zentner, F. Voldoire, D. Clouteau et D. Castro-Cruz, «Enhanced Seismic Response Prediction of Critical Structures via 3D Regional Scale Physics-Based Earthquake Simulation,» Journal of Earthquake Engineering, vol. 27, p. 546–574, January 2022. |
| [2] | J. Bielak, C. Yoshimura, Y. Hisada et A. Fernández, «Domain Reduction Method for Three-Dimensional Earthquake Modeling in Localized Regions, Part I: Theory,» Bulletin of the Seismological Society of America, vol. 93, p. 825–840, 2003. |
| [3] | J. A. Abell, N. Orbović, D. B. McCallen et B. Jeremic, «Earthquake soil-structure interaction of nuclear power plants, differences in response to 3D, 3× 1D, and 1D excitations,» Earthquake Engineering & Structural Dynamics, vol. 47, p. 1478–1495, 2018. |
| [4] | B. Poursartip, A. Fathi et J. L. Tassoulas, «Large-scale simulation of seismic wave motion: A review,» Soil Dynamics and Earthquake Engineering, vol. 129, p. 105909, 2020. |
| [5] | D. McCallen, A. Petersson, A. Rodgers, A. Pitarka, M. Miah, F. Petrone, B. Sjogreen, N. Abrahamson et H. Tang, «EQSIM—A multidisciplinary framework for fault-to-structure earthquake simulations on exascale computers part I: Computational models and workflow,» Earthquake Spectra, 2020. |
| [6] | D. McCallen, F. Petrone, M. Miah, A. Pitarka, A. Rodgers et N. Abrahamson, «EQSIM—A multidisciplinary framework for fault-to-structure earthquake simulations on exascale computers, part II: Regional simulations of building response,» Earthquake Spectra, 2020. |
| [7] | F. De Martin, E. Bourdon, G. Courrioux, E. Foerster, A. Lemoine et A. Roulle, «From Geology to Realistic Large-Scale Spectral-Element Earthquake Simulations in the Pointe-à-Pitre Region,» chez 19ème Conférence géologique de la Caraïbe(19th Caribbean Geological Conference), Le Gosier, Guadeloupe, France, 2011. |
| [8] | E. Cushing, F. Hollender, D. Moiriat, C. Guyonnet‐Benaize, N. Theodoulidis, E. Pons-Branchu, S. Sépulcre, P.-Y. Bard, C. Cornou, A. Dechamp, A. Marsical et Z. Roumelioti, «Building a three dimensional model of the active Plio-Quaternary basin of Argostoli (Cephalonia Island, Greece): An integrated geophysical and geological approach,» Engineering Geology, vol. 265, p. 105441, November 2019. |
| [9] | J. A. Ruiz, D. Baumont, P. Bernard et C. Berge-Thierry, «Modelling directivity of strong ground motion with a fractal, k⁻², kinematic source model,» Geophysical Journal International, vol. 186, pp. 226-244, 2011. |
| [10] | F. Gallovič, «Modeling Velocity Recordings of the Mw 6.0 South Napa, California, Earthquake: Unilateral Event with Weak High‐Frequency Directivity,» Seismological Research Letters, vol. 87, pp. 2-14, November 2015. |
| [11] | M. Stupazzini, M. Infantino, A. Allmann et R. Paolucci, «Physics-based probabilistic seismic hazard and loss assessment in large urban areas: A simplified application to Istanbul,» Earthquake Engineering & Structural Dynamics, vol. 50, pp. 99-115, 2021. |
| [12] | A. C. Riaño, J. C. Reyes, L. E. Yamín, J. Bielak, R. Taborda et D. Restrepo, «Integration of 3D large‐scale earthquake simulations into the assessment of the seismic risk of Bogota, Colombia,» Earthquake Engineering & Structural Dynamics, vol. 50, p. 155–176, January 2021. |
| [13] | M. Ghaemian, A. Noorzad et H. Mohammadnezhad, «Assessment of Foundation Mass and Earthquake Input Mechanism Effect on Dam–Reservoir–Foundation System Response,» International Journal of Civil Engineering, vol. 17, p. 473–480, April 2019. |
| [14] | G. D. Manolis, «Stochastic soil dynamics,» Soil Dynamics and Earthquake Engineering, vol. 22, p. 3–15, January 2002. |
| [15] | P. Sochala, F. De Martin et O. Le Maître, «MODEL REDUCTION FOR LARGE-SCALE EARTHQUAKE SIMULATION IN AN UNCERTAIN 3D MEDIUM,» International Journal for Uncertainty Quantification, vol. 10, p. 101–127, 2020. |
| [16] | F. Lehmann, F. Gatti, M. Bertin et D. Clouteau, «Synthetic ground motions in heterogeneous geologies: the HEMEW-3D dataset for scientific machine learning,» Earth Syst. Sci. Data Discuss. [preprint], https://doi.org/10.5194/essd-2023-470, in review, January 2024. |
| [17] | P. M. Mai, D. Schorlemmer, M. Page, J. Ampuero, K. Asano, M. Causse, S. Custodio, W. Fan, G. Festa, M. Galis, F. Gallovic, W. Imperatori, M. Käser, D. Malytskyy, R. Okuwaki, F. Pollitz, L. Passone, H. N. T. Razafindrakoto, H. Sekiguchi, S. G. Song, S. N. Somala, K. K. S. Thingbaijam, C. Twardzik, M. van Driel, J. C. Vyas, R. Wang, Y. Yagi et O. Zielke, «The Earthquake‐Source Inversion Validation (SIV) Project,» Seismological Research Letters, vol. 87, p. 690–708, May 2016. |
| [18] | M. Causse, C. Cornou, E. Maufroy, J.-R. Grasso, L. Baillet et E. El Haber, «Exceptional ground motion during the shallow Mw 4.9 2019 Le Teil earthquake, France,» Communications Earth & Environment, vol. 2, January 2021. |
| [19] | A. M.-F. R. Fernando Lopez-caballero, «Uncertainty and sensitivity analysis of laboratory test simulations using an elastoplastic model,» chez Numerical Methods in Geotechnical Engineering, CRC Press, 2010, p. 135–140. |

