Contact : Fernando Lopez-Caballero – CentraleSupélec :
fernando.lopez-caballero@centralesupelec.fr
Paris-Saclay University, Laboratoire MSS-Mat.
CNRS UMR 8579, CentraleSupélec, Gif-Sur-Yvette, France.
1. Introduction
In earthquake engineering practice, the local ground response, basin effects, and surface topographic effects are known as “site effects”. Those effects are related with the influence of shallow soils (e.g. in the order of tens to hundreds of meters) on the propagated waves. In practice, to quantify site effects, either empirical models or wave
propagation analysis are used. Such analysis can be implemented for site-specific cases or for site factors in general [10, 3]. In order to perform this kind of analysis for a site-specific evaluation, it is necessary to know i) the geometry and stratigraphy of the site ; ii) the well characterization of the soil properties (i.e. shear-wave velocity, unit weight, modulus reduction, and damping) from geotechnical or geophysical tests ; iii) ground motions recorded at the site of interest (i.e. downhole or outcrop) ; and iv) the choice of soil material model (i.e. Equivalent-linear or Non-linear) [8, 5, 10, 9, among others].
The most common assumption to simulate ground response effects is to perform one-dimensional wave propagation analysis using : i) Horizontal and homogeneous layers ; ii) Vertical incidence of planar SH waves ; and iii) Total stress analysis (i.e. no pore water pressure generation). As expected, those hypothesis simplify the complexity of the site response related to soil heterogeneity and incident wave propagation among others.
Recently, Régnier et al. [9] performed an international benchmark on 1D Nonlinear SiteResponse Analysis using two real sites of the Japanese strong-motion networks KiK-net and Port and Airport Research Institute (PARI). The studied sites were characterized using both in-situ and laboratory measurements of the soil properties. At each site, sets of input motions
were selected to represent different peak ground acceleration and frequency content. The key points from this study were :
- the code-to-code variability given by the standard deviation of the computed surfaceresponse spectra is around 0.1 (in log10 scale) regardless of the site and input motions ;
- large influence of the numerical methods is observed on site-effect assessment ;
- site specific measurements are of primary importance for defining the input data in site response analysis ;
- the way the input motions are applied at the base of the numerical model (i.e. borehole condition) is crucial ;
Some of the discrepancies between predicted and observed site responses could result from the i) errors in the seismic property estimates, namely, both the number and the quality of laboratory tests ; ii) the simplification of the propagation path of the incident waves. It is clear that the accuracy of such predictions remains limited due to large uncertainties on the data to be introduced in the model and even very extensive geophysical surveys fail at reducing the resulting uncertainties on the predicted ground motion. In addition, such large-scale surveys cannot be conducted for all practical cases.
2. Objectives
The main objectives of the proposed research are :
- to perform a regional model (e.g. 2D or 3D) that simulates the seismic phenomenon from the source to the site so as to better analyse the obtained incident signals at the bottom of the one-dimensional wave propagation model ;
- to propose a virtual vertical array site to perform blind predictions using a one-dimensional wave propagation model ;
- to build up a multi-tool virtual laboratory and in-situ test to calibrate the required few well-known parameters for non-linear soil models ;
- to identify and to optimise the minimum number of laboratory and in-situ tests needed to obtain an accurate response using simplified wave propagation models (e.g. equivalentlinear or Non-linear models) ;
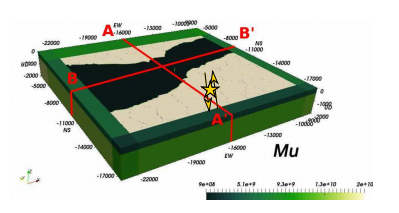
Figure 1 – SEM3D model of the Mygdonian basin for a 3D local scale model.
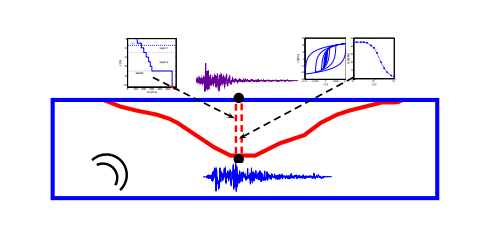
Figure 2 – Schematic representation of the proposed work for a 2D local scale model.
3. Work Time Schedule
The project length is 12 months in addition to 2 months for the writing and the review of the final report.
Références
[1] Aubry, D., Hujeux, J.-C., Lassoudière, F., and Meimon, Y. (1982). A double memory model with multiple mechanisms for cyclic soil behaviour. In Int. Symp. Num. Mod. Geomech, pages
3–13. Balkema.
[2] Aubry, D. and Modaressi, A. (1996). GEFdyn. Manuel scientifique, Ecole Centrale Paris, LMSS-Mat.
[3] Bonilla, L. F., Gueguen, P., Lopez-Caballero, F., Mercerat, D. E., and Gélis, C. (2017). Prediction of non-linear site response using downhole array data and numerical modeling : the Belleplaine (Guadeloupe) case study. Physics and Chemistry of the Earth, Parts A/B/C, 98(1) : 107–118.
[4] Fathi, A., Poursartip, B., Stokoe II, K. H., and Kallivokas, L. F. (2016). Three-dimensional p- and s-wave velocity profiling of geotechnical sites using full-waveform inversion driven by field data. Soil Dynamics and Earthquake Engineering, 87 :63 – 81.
[5] Foerster, E. and Modaressi, H. (2007). Nonlinear numerical method for earthquake site response analysis ii — case studies. Bulletin of Earthquake Engineering, 5(3) :325–345.
[6] Gatti, F., Lopez-Caballero, F., Clouteau, D., and Paolucci, R. (2018). On the effect of the 3-D regional geology on the seismic design of critical structures : the case of the KashiwazakiKariwa Nuclear Power Plant. Geophysical Journal International, 213(2) :1073–1092.
[7] Hujeux, J.-C. (1985). Une loi de comportement pour le chargement cyclique des sols. In Génie Parasismique, pages 278–302. V. Davidovici, Presses ENPC, France.
[8] Lopez-Caballero, F., Modaressi Farahmand-Razavi, A., and Modaressi, H. (2007). Nonlinear numerical method for earthquake site response analysis i- elastoplastic cyclic model &
parameter identification strategy. Bulletin of Earthquake Engineering, 5(3) :303–323.
[9] Régnier, J., Bonilla, L., Bard, P., Bertrand, E., Hollender, F., Kawase, H., Sicilia, D., Arduino, P., Amorosi, A., Asimaki, D., Boldini, D., Chen, L., Chiaradonna, A., DeMartin, F., Elgamal, A., Falcone, G., Foerster, E., Foti, S., Garini, E., Gazetas, G., Gélis, C., Ghofrani, A., Giannakou, A., Gingery, J., Glinsky, N., Harmon, J., Hashash, Y., Iai, S., Kramer, S., Kontoe, S., Kristek, J., Lanzo, G., Lernia, A. d., Lopez-Caballero, F., Marot, M., McAllister, G., Diego Mercerat, E., Moczo, P., Montoya-Noguera, S., Musgrove, M., Nieto-Ferro, A., Pagliaroli, A., Passeri, F., Richterova, A., Sajana, S., Santisi d’Avila, M. P., Shi, J., Silvestri, F., Taiebat, M., Tropeano, G., Vandeputte, D., and Verrucci, L. (2018). Prenolin : International benchmark on 1d nonlinear site-response analysis-validation phase exercise. Bulletin of the Seismological Society of America, 108(2) :876–900.
[10] Stewart, J. P., Kwok, A. O., Hashash, Y., Matasovic, N., and Pike, R. (2008). Benchmarking of nonlinear geotechnical ground response analysis procedures. Technical report, PEER Report No. 2008/04, Pacific Earthquake Engineering Research Center, University of California, Berkeley, CA.

